
已知函數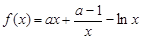
(1)當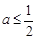 時,試討論函數
時,試討論函數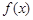 的單調性;
的單調性;
(2)證明:對任意的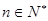 ,有
,有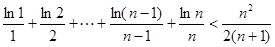 .
.
(1)①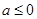 時,
時, 在(0,1)是增函數,在
在(0,1)是增函數,在 是減函數;
是減函數;
②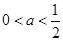 時,
時, 在(0,1),
在(0,1),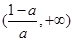 是增函數,在
是增函數,在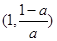 是減函數;
是減函數;
③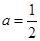 時,
時, 在
在 是增函數.
是增函數.
(2)見解析.
解析試題分析:(1)求導數得到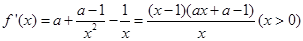 ,而后根據兩個駐點的大小比較,分以下三種情況討論.
,而后根據兩個駐點的大小比較,分以下三種情況討論.
①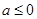 時,
時, 在(0,1)是增函數,在
在(0,1)是增函數,在 是減函數;
是減函數;
②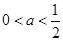 時,
時, 在(0,1),
在(0,1),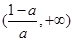 是增函數,在
是增函數,在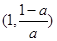 是減函數;
是減函數;
③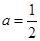 時,
時, 在
在 是增函數.
是增函數.
(2)注意到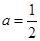 時,
時, 在
在 是增函數
是增函數
當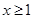 時,有
時,有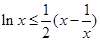 .從而得到:對任意的
.從而得到:對任意的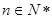 ,有
,有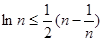
通過構造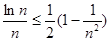 ,并放縮得到
,并放縮得到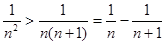
利用裂項相消法求和,證得不等式。涉及數列問題,往往通過“放縮、求和”轉化得到求證不等式.
試題解析:(1)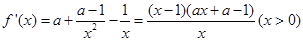 1分
1分
①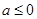 時,
時, 在(0,1)是增函數,在
在(0,1)是增函數,在 是減函數; 3分
是減函數; 3分
②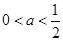 時,
時, 在(0,1),
在(0,1),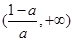 是增函數,在
是增函數,在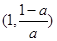 是減函數; 5分
是減函數; 5分
③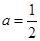 時,
時, 在
在 是增函數. 6分
是增函數. 6分
(2)由(1)知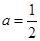 時,
時, 在
在 是增函數
是增函數
當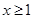 時,
時,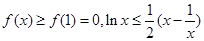 .
.
對任意的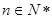 ,有
,有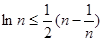
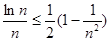 8分
8分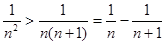 10分
10分
所以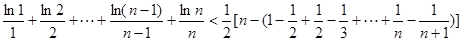
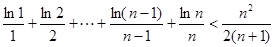 12分
12分
考點:應用導數研究函數的單調性,應用導數證明不等式,“裂項相消法”求和.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:解答題
已知函數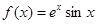 .
.
(Ⅰ)求函數 的單調區間;
的單調區間;
(Ⅱ)如果對于任意的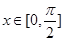 ,
,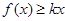 總成立,求實數
總成立,求實數 的取值范圍;
的取值范圍;
(Ⅲ)設函數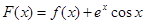 ,
,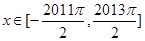 ,過點
,過點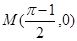 作函數
作函數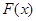 圖象的所有切線,令各切點得橫坐標構成數列
圖象的所有切線,令各切點得橫坐標構成數列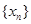 ,求數列
,求數列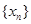 的所有項之和
的所有項之和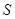 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 的導函數
的導函數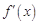 是二次函數,當
是二次函數,當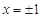 時,
時, 有極值,且極大值為2,
有極值,且極大值為2,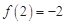 .
.
(1)求函數 的解析式;
的解析式;
(2)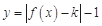 有兩個零點,求實數
有兩個零點,求實數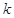 的取值范圍;
的取值范圍;
(3)設函數 ,若存在實數
,若存在實數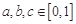 ,使得
,使得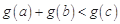 ,求
,求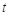 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com