
(本小題滿分14分)
(1)已知正項等差數列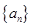 的前
的前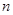 項和為
項和為 ,若
,若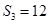 ,且
,且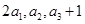 成等比數列.求
成等比數列.求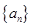 的通項公式.
的通項公式.
(2)數列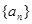 中,
中,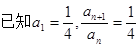 ,
, .求
.求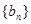 的通項公式.
的通項公式.
(1)  ; (2)
; (2) 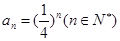 ,
, .
.
解析試題分析:(1)根據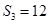 ,且
,且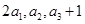 成等比數列可得到關于a1和d的兩個方程,進而得到
成等比數列可得到關于a1和d的兩個方程,進而得到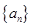 的通項公式.
的通項公式.
(2) 由 ,可知數列
,可知數列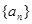 是首項為
是首項為 ,公比為
,公比為 的等比數列,因而可求出
的等比數列,因而可求出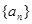 的通項公式,進一步根據對數的運算性質可求出bn.
的通項公式,進一步根據對數的運算性質可求出bn.
(1)記 的公差為
的公差為
∵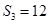 ,即
,即 ∴
∴ ,所以
,所以 ·······2分
·······2分
又 ,
, ,
,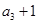 成等比數列,
成等比數列,
∴ ,即
,即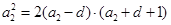 ·······4分
·······4分
解得, 或
或 (舍去),
(舍去),
∴ ,故
,故 ·······7分
·······7分
(2) 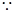

∴數列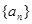 是首項為
是首項為 ,公比為
,公比為 的等比數列 ·······2分
的等比數列 ·······2分
故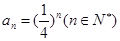 ·······4分
·······4分 ·······5分
·······5分
∴ . ·······7分
. ·······7分
考點:等差數列的前n項和,等比數列的定義,對數的運算性質.
點評:利用方程的思想來考慮如何求a1和d.這樣須建立關于它們倆個的兩個方程.由于 顯然可確定
顯然可確定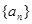 是首項為
是首項為 ,公比為
,公比為 的等比數列,到此問題基本得解.
的等比數列,到此問題基本得解.


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知數列 的各項排成如圖所示的三角形數陣,數陣中每一行的第一個數
的各項排成如圖所示的三角形數陣,數陣中每一行的第一個數 構成等差數列
構成等差數列 ,
, 是
是 的前n項和,且
的前n項和,且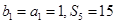

( I )若數陣中從第三行開始每行中的數按從左到右的順序均構成公比為正數的等比數列,且公比相等,已知 ,求
,求 的值;
的值;
(Ⅱ)設 ,求
,求 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com