
��֪���c(di��n)��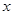 �S�ϵęE�A
�S�ϵęE�A ���p����
���p���� ���x���ʻ��鵹��(sh��)�������ڵ�һ�����c(di��n)������(bi��o)��
���x���ʻ��鵹��(sh��)�������ڵ�һ�����c(di��n)������(bi��o)�� ���O(sh��)ֱ��
���O(sh��)ֱ��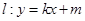 ������
������ ������(sh��)��.
������(sh��)��.
��1��ԇ��E�A ���p����
���p���� �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����ֱ�� �c�E�A
�c�E�A ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n) ���c�p����
���c�p���� ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n) �����Ƿ����ֱ��
�����Ƿ����ֱ�� ��ʹ������
��ʹ������ �������ڣ�ָ���@�ӵ�ֱ���ж��ٗl���������ڣ�Ո�f������.
�������ڣ�ָ���@�ӵ�ֱ���ж��ٗl���������ڣ�Ո�f������.
��1���E�A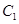 �飺
�飺
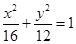 ���p����
���p����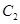 �飺
�飺 ��2�����ڣ��M��l����ֱ������9�l.
��2�����ڣ��M��l����ֱ������9�l.
��������
ԇ�}��������1�����c(di��n)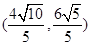 ����
���� ��������E�A
��������E�A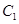 �ķ��̣�ͨ�^�E�A
�ķ��̣�ͨ�^�E�A ���x��������p����
���x��������p����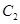 ���x���ʣ�(li��n)���x���ʺ��p�����ķ��̣����
���x���ʣ�(li��n)���x���ʺ��p�����ķ��̣���� ����2����?y��n)�ֱ��
����2����?y��n)�ֱ��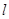 �c�E�A
�c�E�A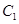 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)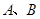 ������(li��n)��ֱ���͙E�A���̣���ȥ
������(li��n)��ֱ���͙E�A���̣���ȥ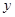 ���������̼���.
���������̼���.
ԇ�}��������1�����c(di��n)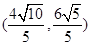 ����
���� ���
���
���E�A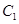 �飺
�飺
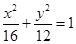 ��
��2�֣�
��
��2�֣�
�E�A ���x���ʞ�
���x���ʞ�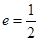 ���p����
���p����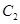 ���x���ʞ�
���x���ʞ� ��
��3�֣�
��
��3�֣�
��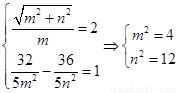 ��
��
���p����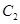 �飺
�飺 ��6�֣�
��6�֣�
��2����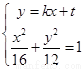 ��ȥ
��ȥ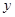 ���������ã�
���������ã�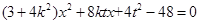
�O(sh��) ��
�� ���t
���t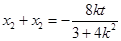
 ��
��8�֣�
��
��8�֣�
��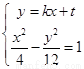 ��ȥ
��ȥ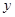 ���������ã�
���������ã�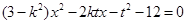
�O(sh��)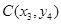 ��
�� ���t
���t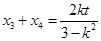
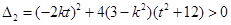 ��
��10�֣�
��
��10�֣�
��?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013091800251940095871/SYS201309180027059791627819_DA.files/image028.png">������ ��
��
�� �ã�
�ã� ��
��
���� ��
��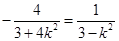 ������ʽ���
������ʽ���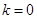 ��
��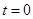 ��
��
��(d��ng)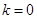 �r(sh��)���ɢٺ͢ڵ�
�r(sh��)���ɢٺ͢ڵ�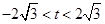 ����
���� ������(sh��)��
������(sh��)��
���� ��ֵ��
��ֵ��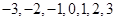
��(d��ng)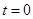 ���ɢٺ͢ڵ�
���ɢٺ͢ڵ�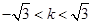 ����
���� ������(sh��)������
������(sh��)������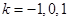 ��
��
���ǝM��l����ֱ������9�l�� ��13�֣�
���c(di��n)��1.��E�A���p�����ķ���.


 ��ĩ�_��100�ք�(chu��ng)�½����ȫԇ��ϵ�д�
��ĩ�_��100�ք�(chu��ng)�½����ȫԇ��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
��08��B�T����Z�W(xu��)Уģ�M����12�֣�
��֪���c(di��n)��![]() �S�ϵęE�A
�S�ϵęE�A![]() �����ăɂ�(g��)���c(di��n).
�����ăɂ�(g��)���c(di��n).
�������E�A�ϴ���һ�c(di��n)P��ʹ��![]() ԇ��
ԇ��![]() ��ȡֵ����;
��ȡֵ����;
�������E�A���x���ʞ�![]() ����(j��ng)�^�ҽ��c(di��n)
����(j��ng)�^�ҽ��c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A�ཻ��A��B���c(di��n),��
�c�E�A�ཻ��A��B���c(di��n),��![]() ,��ֱ��
,��ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2014�ý����ϲ���һ���鶼�������ЌW(xu��)�߶������Д�(sh��)�W(xu��)ԇ���������棩 �}�ͣ��x���}
��֪���c(di��n)�� �S�ϵęE�A���x���ʞ�
�S�ϵęE�A���x���ʞ� �������L�S�L���ڈA
�������L�S�L���ڈA �İ돽���t�E�A�Ę�(bi��o)��(zh��n)�����ǣ� ��
�İ돽���t�E�A�Ę�(bi��o)��(zh��n)�����ǣ� ��
A�� B.
B.  C.
C.
 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011-2012�W(xu��)���㽭ʡ�����W(xu��)��2���¿����Ɣ�(sh��)�W(xu��)ԇ�� �}�ͣ�����}
�����}�M��15�֣���֪���c(di��n)�� �S�ϵęE�A
�S�ϵęE�A �^�c(di��n)
�^�c(di��n) �����x���ʞ�
�����x���ʞ� ,
, ��E�A
��E�A ������c(di��n).
������c(di��n).
������E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
������֪�^�c(di��n) ��ֱ��
��ֱ�� �c�E�A
�c�E�A ����
���� ��
�� ���c(di��n).
���c(di��n).
��������ֱ�� ��ֱ��
��ֱ�� �S����
�S���� �Ĵ�С;
�Ĵ�С;
��������ֱ�� �c
�c �S����ֱ���Ƿ����ֱ��
�S����ֱ���Ƿ����ֱ�� ʹ��
ʹ��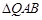 ����������Σ�������ڣ����ֱ��
����������Σ�������ڣ����ֱ�� �ķ��̣���������ڣ�Ո�f������.
�ķ��̣���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2010�������ʡ�߶��W(xu��)�����п�ԇ��(sh��)�W(xu��)���ģ� �}�ͣ��x���}
1.
��֪���c(di��n)�� �S�ϵęE�A
�S�ϵęE�A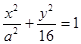 �ăɂ�(g��)���c(di��n)�քe��
�ăɂ�(g��)���c(di��n)�քe�� , ��
, ��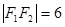 ����
���� �^���c(di��n)
�^���c(di��n) ���t
���t �����L��
�����L��
A��  B��
B��  C��
C��  D��
D�� 
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com