
已知函數 ,
, .
.
(I)求函數 的單調區間;
的單調區間;
(Ⅱ)當 時,函數
時,函數 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(Ⅲ)設正實數 滿足
滿足 ,求證:
,求證: .
.
 當
當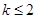 時,只有單調遞增區間
時,只有單調遞增區間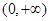 ;當
;當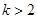 時,單調遞增區間為
時,單調遞增區間為 ,
,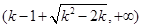 ,單調遞減區間為
,單調遞減區間為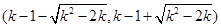 .
.
 ;
;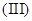 詳見解析.
詳見解析.
解析試題分析: 先求出
先求出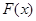 的導數,討論
的導數,討論 ,利用導數的正負與函數單調性得關系求出單調區間;
,利用導數的正負與函數單調性得關系求出單調區間; 當x>1時,函數f(x)>g(x)恒成立轉化為
當x>1時,函數f(x)>g(x)恒成立轉化為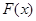 >0恒成立.結合第
>0恒成立.結合第 問討論的單調區間得出
問討論的單調區間得出 的范圍;
的范圍;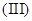 結合第
結合第 問,令
問,令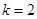 ,
,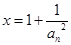 ,所以
,所以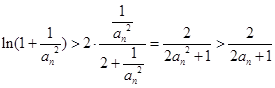 ,再利用柯西不等式,
,再利用柯西不等式,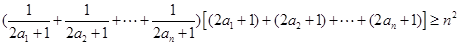 ,其中由條件
,其中由條件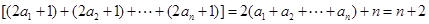 .最后得證.
.最后得證.
試題解析:(Ⅰ)易知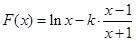 ,定義域是
,定義域是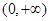 .
.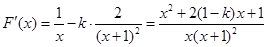 1分
1分
由 的判別式
的判別式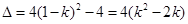
①當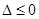 即
即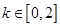 時,
時,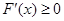 恒成立,則
恒成立,則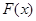 在
在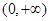 單調遞增 2分
單調遞增 2分
②當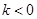 時,
時,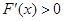 在
在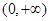 恒成立,則
恒成立,則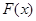 在
在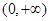 單調遞增 3分
單調遞增 3分
③當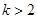 時,方程
時,方程 的兩正根為
的兩正根為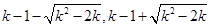
則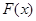 在
在 單調遞增,
單調遞增,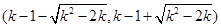 單調遞減,
單調遞減,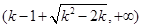 單調遞增
單調遞增
綜上,當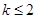 時,只有單調遞增區間
時,只有單調遞增區間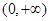
當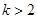 時,單調遞增區間為
時,單調遞增區間為 ,
,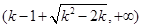
單調遞減區間為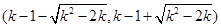 5分
5分
(Ⅱ)即 時,
時,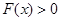 恒成立
恒成立
當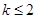 時,
時,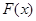 在
在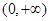 單調遞增 ∴當
單調遞增 ∴當 時,
時,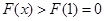 滿足條件 7分
滿足條件 7分
當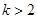 時,
時,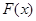 在
在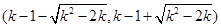 單調遞減
單調遞減
則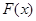 在
在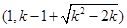 單調遞減
單調遞減
此時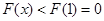 不滿足條件
不滿足條件
故實數 的取值范圍為
的取值范圍為 9分
9分
(Ⅲ)由(2)知,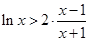 在
在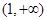 恒成立
恒成立
令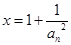 則
則  10分
10分
∴ 11分
11分
又
其中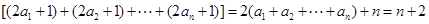
∴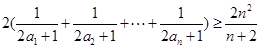 &nb
&nb


科目:高中數學 來源: 題型:解答題
揚州某地區要建造一條防洪堤,其橫斷面為等腰梯形,腰與底邊成角為 (如圖),考慮到防洪堤堅固性及石塊用料等因素,設計其橫斷面要求面積為
(如圖),考慮到防洪堤堅固性及石塊用料等因素,設計其橫斷面要求面積為 平方米,且高度不低于
平方米,且高度不低于 米.記防洪堤橫斷面的腰長為
米.記防洪堤橫斷面的腰長為 (米),外周長(梯形的上底線段
(米),外周長(梯形的上底線段 與兩腰長的和)為
與兩腰長的和)為 (米).
(米).
⑴求 關于
關于 的函數關系式,并指出其定義域;
的函數關系式,并指出其定義域;
⑵要使防洪堤橫斷面的外周長不超過 米,則其腰長
米,則其腰長 應在什么范圍內?
應在什么范圍內?
⑶當防洪堤的腰長 為多少米時,堤的上面與兩側面的水泥用料最省(即斷面的外周長最小)?求此時外周長的值.
為多少米時,堤的上面與兩側面的水泥用料最省(即斷面的外周長最小)?求此時外周長的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數f(x)(x∈D),若x∈D時,恒有 >
> 成立,則稱函數
成立,則稱函數 是D上的J函數.
是D上的J函數.
(Ⅰ)當函數f(x)=m lnx是J函數時,求m的取值范圍;
lnx是J函數時,求m的取值范圍;
(Ⅱ)若函數g(x)為(0,+∞)上的J函數,
試比較g(a)與 g(1)的大小;
g(1)的大小;
求證:對于任意大于1的實數x1,x2,x3, ,xn,均有g(ln(x1+x2+ +xn))
>g(lnx1)+g(lnx2)+ +g(lnxn).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com