
已知 .
.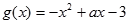 .
.
(1)求函數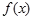 在區間
在區間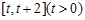 上的最小值;
上的最小值;
(2)對一切實數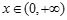 ,
,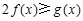 恒成立,求實數
恒成立,求實數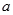 的取值范圍;
的取值范圍;
(3) 證明對一切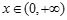 ,
, 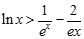 恒成立.
恒成立.
(1)見解析;(2)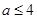 ;(3)見解析.
;(3)見解析.
解析試題分析:(1)對于研究非常規的初等函數的最值問題,往往都需要求函數的導數.根據函數導數的正負判斷函數的單調性,利用單調性求函數在某個區間上的最值;(2)恒成立問題,一般都需要將常數和變量分離開來(分離常數法)轉化為最值問題處理;(3)證明不等式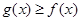 恒成立問題,往往將不等式轉化為函數
恒成立問題,往往將不等式轉化為函數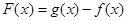 來證明
來證明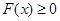 恒成立問題.但有些時候這樣轉化后不等會乃然很難實現證明,還需對不等式經行恒等變形以達到化簡不等式的目的,然后再證.
恒成立問題.但有些時候這樣轉化后不等會乃然很難實現證明,還需對不等式經行恒等變形以達到化簡不等式的目的,然后再證.
試題解析:⑴ 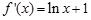 ,當
,當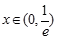 ,
,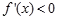 ,
,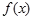 單調遞減,
單調遞減,
當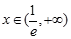 ,
,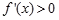 ,
,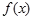 單調遞增. 1分
單調遞增. 1分
(由于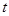 的取值范圍不同導致
的取值范圍不同導致 所處的區間函數單調性不同,故對
所處的區間函數單調性不同,故對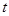 經行分類討論.)
經行分類討論.)
① 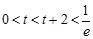 ,t無解; 2分
,t無解; 2分
② 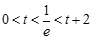 ,即
,即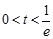 時,
時,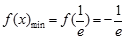 3分
3分
③ 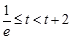 ,即
,即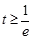 時,
時,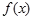 在
在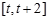 上單調遞增,
上單調遞增,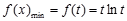 ;
;
所以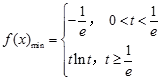 5分
5分
由題可知: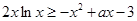 ,則
,則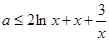 .因對于
.因對于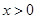 ,
,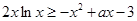 恒成立,故
恒成立,故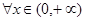 ,
,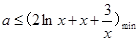
設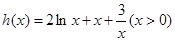 ,則
,則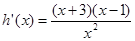 .
.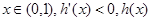 單調遞增,
單調遞增,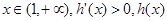 單調遞減.
單調遞減.
所以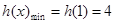 ,即
,即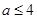 .
.
問題等價于證明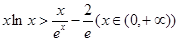 (為了利用第(1)小問結論,并考慮到作差做函數證明不方便,下證
(為了利用第(1)小問結論,并考慮到作差做函數證明不方便,下證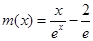 的最值與
的最值與 最值的關系.)
最值的關系.)
由(1)可知 在
在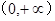 的最小值是
的最小值是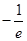 ,當且僅當
,當且僅當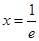 時取到.
時取到.
設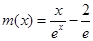 ,則
,則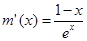 ,易得
,易得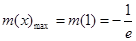 ,當且僅當
,當且僅當 時取到.
時取到.
從而對于一切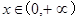 ,都有
,都有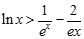 恒成立.
恒成立.
考點:(1)含參量函數最值的討論;(2)含參恒成立問題,參數取值范圍;(3)利用倒數證明不等式.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:解答題
已知函數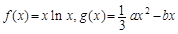 ,其中a,b∈R
,其中a,b∈R
(1)求函數f(x)的最小值;
(2)當a>0,且a為常數時,若函數h(x)=x[g(x)+1]對任意的x1>x2≥4,總有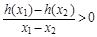 成立,試用a表示出b的取值范圍;
成立,試用a表示出b的取值范圍;
(3)當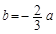 時,若
時,若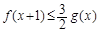 對x∈[0,+∞)恒成立,求a的最小值.
對x∈[0,+∞)恒成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
如圖是函數y=f(x)的導函數的圖象,給出下面四個判斷.
①f(x)在區間[-2,-1]上是增函數;
②x= -1是f(x)的極小值點;
-1是f(x)的極小值點;
③f(x)在區間[-1,2]上是增函數,在區間[2,4]上是減函數;
④x=3是f(x)的極小值點.
其中,所有正確判斷的序號是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com