
如圖,四棱錐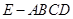 中,面
中,面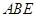
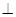 面
面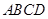 ,底面
,底面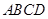 是直角梯形,側(cè)面
是直角梯形,側(cè)面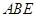 是等腰直角三角形.且
是等腰直角三角形.且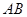 ∥
∥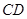 ,
,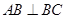 ,
,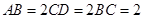 ,
,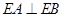 .
.
(1)判斷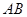 與
與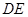 的位置關(guān)系;
的位置關(guān)系;
(2)求三棱錐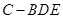 的體積;
的體積;
(3)若點(diǎn)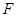 是線段
是線段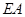 上一點(diǎn),當(dāng)
上一點(diǎn),當(dāng)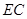 //平面
//平面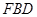 時(shí),求
時(shí),求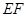 的長.
的長.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析試題分析:本題以四棱錐為幾何背景考查線線垂直、線面垂直、線面平行、線線平行的判定,在解題過程中還遇到了等腰直角三角形和直角梯形以及相似三角形等基礎(chǔ)知識(shí),考查空間想象能力和推理論證能力.第一問,取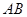 中點(diǎn)
中點(diǎn) ,連結(jié)
,連結(jié) ,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/41/a/x5ao32.png" style="vertical-align:middle;" />是等腰直角三角形,所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/41/a/x5ao32.png" style="vertical-align:middle;" />是等腰直角三角形,所以 ,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/f8/e/1nnuc2.png" style="vertical-align:middle;" />是直角梯形且
,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/f8/e/1nnuc2.png" style="vertical-align:middle;" />是直角梯形且 ,所以四邊形
,所以四邊形 為正方形,所以
為正方形,所以 ,所以
,所以 平面
平面 ,所以
,所以 ;第二問,先利用面面垂直,可得到線面垂直,得到錐體的高
;第二問,先利用面面垂直,可得到線面垂直,得到錐體的高 ,用等體積法將
,用等體積法將 轉(zhuǎn)化為
轉(zhuǎn)化為 ,再利用體積公式求值;第三問,先在面內(nèi)找到線
,再利用體積公式求值;第三問,先在面內(nèi)找到線 ,這是由于
,這是由于 // 平面
// 平面 ,再利用相似三角形,得到邊長的關(guān)系,所以
,再利用相似三角形,得到邊長的關(guān)系,所以 ,所以
,所以 .
.
試題解析:(1)證明:取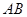 中點(diǎn)
中點(diǎn) ,連結(jié)
,連結(jié) ,
, .
.
因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/58/7/18rw74.png" style="vertical-align:middle;" />,所以 .
.
因?yàn)樗倪呅?img src="http://thumb.zyjl.cn/pic5/tikupic/f8/e/1nnuc2.png" style="vertical-align:middle;" />為直角梯形, ,
,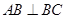 ,
,
所以四邊形 為正方形,所以
為正方形,所以 .
.
所以 平面
平面 . 所以
. 所以  . 4分
. 4分
(2)由 ,面
,面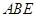
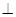 面
面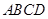 易得
易得
所以, 8分
8分
(3)解:連接 交于點(diǎn),面
交于點(diǎn),面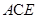
 面
面 .
.
因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/2e/f/vj6hd2.png" style="vertical-align:middle;" />//平面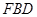 ,所以
,所以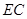 //
// .
.
在梯形 中,有
中,有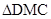 與
與 相似,
相似,
可得
所以,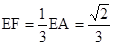 12分
12分
考點(diǎn):1.線面垂直的判定定理;2.等體積法;3.相似三角形的性質(zhì).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D為AB的中點(diǎn).
(Ⅰ)求異面直線CC1和AB的距離;
(Ⅱ)若AB1⊥A1C,求二面角A1-CD-B1的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,已知三棱錐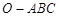 的側(cè)棱
的側(cè)棱 兩兩垂直,且
兩兩垂直,且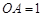 ,
,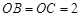 ,
,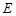 是
是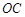 的中點(diǎn)。
的中點(diǎn)。
(1)求異面直線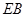 與
與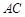 所成角的余弦值;
所成角的余弦值;
(2)求直線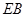 和平面
和平面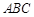 的所成角的正弦值。
的所成角的正弦值。
(3)求點(diǎn)E到面ABC的距離。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(如圖1)在平面四邊形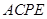 中,
中,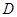 為
為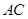 中點(diǎn),
中點(diǎn),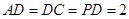 ,
,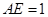 ,且
,且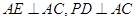 ,現(xiàn)沿
,現(xiàn)沿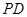 折起使
折起使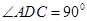 ,得到立體圖形(如圖2),又B為平面ADC內(nèi)一點(diǎn),并且ABCD為正方形,設(shè)F,G,H分別為PB,EB,PC的中點(diǎn).
,得到立體圖形(如圖2),又B為平面ADC內(nèi)一點(diǎn),并且ABCD為正方形,設(shè)F,G,H分別為PB,EB,PC的中點(diǎn).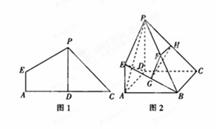
(1)求三棱錐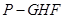 的體積;
的體積;
(2)在線段PC上是否存在一點(diǎn)M,使直線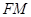 與直線
與直線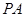 所成角為
所成角為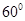 ?若存在,求出線段的長;若不存在,請(qǐng)說明理由.
?若存在,求出線段的長;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
(1)求證:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求點(diǎn)B到平面MAC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在斜三棱柱ABC-A1B1C1中,側(cè)面AA1B1B⊥底面ABC,側(cè)棱AA1與底面ABC成60°的 角,AA1=2.底面ABC是邊長為2的正三角形,其重心為G點(diǎn),E是線段BC1上一點(diǎn),且BE=3BC1.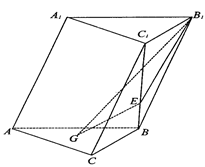

(1)求證:GE∥側(cè)面AA1B1B;
(2)求平面B1GE與底面ABC所成銳二面角的正切值;
(3)求點(diǎn)B到平面B1GE的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(1)如圖,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求證:P,Q,R三點(diǎn)共線.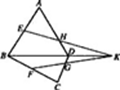
(2)如圖,空間四邊形ABCD中,E,F分別是AB和CB上的點(diǎn),G,H分別是CD和AD上的點(diǎn), 且EH與FG相交于點(diǎn)K. 求證:EH,BD,FG三條直線相交于同一點(diǎn).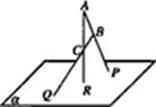
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直三棱柱ABC-A1B1C1中,點(diǎn)M是A1B的中點(diǎn),點(diǎn)N是B1C的中點(diǎn),連接MN 
(Ⅰ)證明:MN//平面ABC;
(Ⅱ)若AB=1,AC=AA1=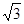 ,BC=2,求二面角A—A1C—B的余弦值的大小
,BC=2,求二面角A—A1C—B的余弦值的大小
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com