
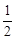 成等比數列.
成等比數列.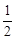 成等比數列,∴Sn2=an·(Sn-
成等比數列,∴Sn2=an·(Sn-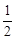 )(n≥2) (*)
)(n≥2) (*)
 ,S3=
,S3= +a3代入(*)式得:a3=-
+a3代入(*)式得:a3=-
 ,由此可推出:an=
,由此可推出:an=
 成立
成立 ·(Sk-
·(Sk-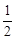 )
) (舍)
(舍)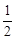 ),得(Sk+ak+1)2=ak+1(ak+1+Sk-
),得(Sk+ak+1)2=ak+1(ak+1+Sk-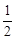 )
)
 對一切n∈N成立.
對一切n∈N成立. .
.

科目:高中數學 來源:不詳 題型:解答題
 是區域
是區域 ,(
,( )內的點,目標函數
)內的點,目標函數 ,
, 的最大值記作
的最大值記作 .若數列
.若數列 的前
的前 項和為
項和為 ,
,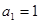 ,且點(
,且點( )在直線
)在直線 上.
上. 為等比數列;
為等比數列; 的前
的前 項和
項和 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
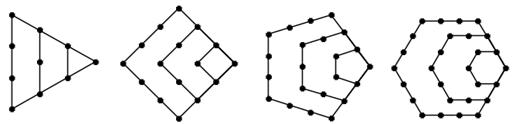
 ,將構圖邊數增加到
,將構圖邊數增加到 可得到“
可得到“ 邊形數列”,記它的第
邊形數列”,記它的第 項為
項為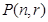 ,
,
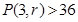 的最小
的最小 的取值;
的取值;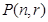 關于
關于 、
、 的解析式;
的解析式; 邊形數列”,它的任意連續兩項的和均為完全平方數,若存在,指出所有滿足條件的數列并證明你的結論;若不存在,請說明理由.
邊形數列”,它的任意連續兩項的和均為完全平方數,若存在,指出所有滿足條件的數列并證明你的結論;若不存在,請說明理由.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
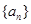 是等積數列,且
是等積數列,且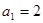 ,公積為5,則這個數列的前
,公積為5,則這個數列的前 項和
項和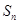 的計算公式為: .
的計算公式為: .查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 知數列{an}的前n項和
知數列{an}的前n項和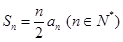 ,且
,且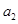 =1,
=1,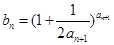
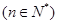 .(I)求數列{an}的通項公式;
.(I)求數列{an}的通項公式;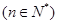 在(0,+∞)上是凹函數,試判斷bn與bn+1的大小;
在(0,+∞)上是凹函數,試判斷bn與bn+1的大小;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com