在數(shù)列
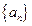
中,
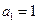
,
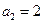
,且
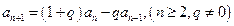
;
(1)設(shè)
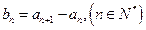
,證明
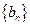
是等比數(shù)列;(2)求數(shù)列
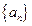
的通項公式;(3)若
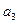
是
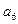
與
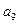
的等差中項,求
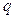
的值,并證明:對任意的
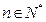
,
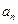
是
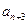
與
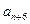
的等差中項;
(1)略(2)

(3)證明略
本題源自等差數(shù)列通項公式的推導(dǎo)。
(1)證明:由題設(shè)
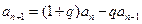
(
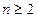
),得
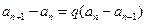
,即
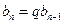
,
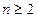
.
又

,
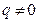
,所以
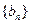
是首項為1,公比為
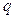
的等比數(shù)列.
(2)由(1)
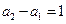
,
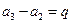
,
……
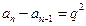
,(
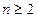
).
將以上各式相加,得

(
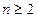
).
所以當
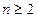
時,

上式對
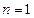
顯然成立.
(3)由(2),當
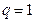
時,顯然
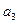
不是
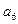
與
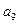
的等差中項,故
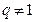
.
由
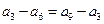
可得

,由
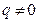
得

, ①
整理得

,解得
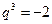
或

(舍去).于是

.
另一方面,
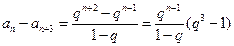
,
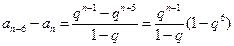
.
由①可得

,
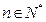
.
所以對任意的
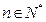
,
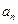
是
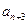
與
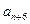
的等差中項.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知正數(shù)數(shù)列
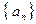
的前
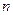
項和為
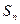
,
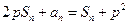
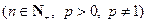
,數(shù)列
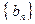
滿足

.(Ⅰ)求數(shù)列
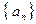
和
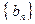
的通項公式; (Ⅱ)當
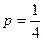
時,
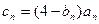
,求數(shù)列
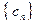
的前
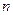
項和
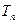
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設(shè){
an}是等差數(shù)列,
bn=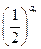
.已知
b1+
b2+
b3=
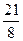
,
b1b2b3=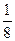 .
.求等差數(shù)列的通項
an.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題16分)已知數(shù)列
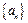
的前n項的和S
n,滿足
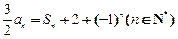
.
(1)求數(shù)列
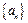
的通項公式.(2)設(shè)
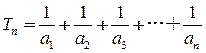
,是否存在正整數(shù)k,使得當n≥3時,
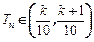
如果存在,求出k;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
對于函數(shù)y=f(x),若x
1+x
2="1," 則f(x
1)+f(x
2)=1,記數(shù)列f(
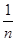
),f(
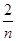
),
……,f(
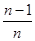
)……,(n≥2,n∈
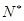
)的前n項的和為S
n ; (1)求S
n; (2)若a
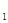
=
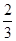
,a
=" "
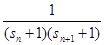
(n≥2,n∈
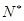
),
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
等差數(shù)列
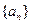
中,
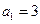
,前
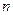
項和為

,等比數(shù)列
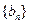
各項均為正數(shù),

,且
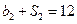
,
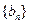
的公比


(1)求
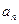
與
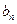
;(2)證明:
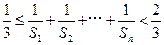

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
某縣位于沙漠地帶,人與自然長期進行著頑強的斗爭,到2009年底全縣的綠化率已達30%。從2010年開始,每年將出現(xiàn)這樣的局面,即原有沙漠面積的16%將被綠化,與此同時,由于各種原因,原有綠化面積的4%又被沙化。
(1)設(shè)全縣面積為1,2001年底綠化面積為a1=,經(jīng)過n年綠化總面積為an+1。
求證:an+1=+an
(2)至少需要多少年(年取整數(shù),lg2=0.3010)的努力,才能使全縣的綠化率達到60%?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知數(shù)列
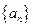
是等差數(shù)列,若
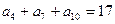
,
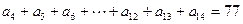
且
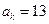
,則
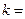
___
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)
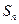
是等差數(shù)列
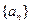
的前
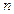
項和,若
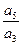
=
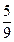
,則
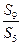
等于

| A.1 | B.-1 | C.2 | D.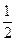  |
查看答案和解析>>

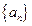 中,
中,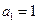 ,
,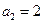 ,且
,且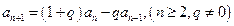 ;
;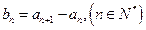 ,證明
,證明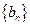 是等比數(shù)列;(2)求數(shù)列
是等比數(shù)列;(2)求數(shù)列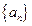 的通項公式;(3)若
的通項公式;(3)若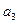 是
是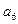 與
與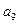 的等差中項,求
的等差中項,求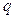 的值,并證明:對任意的
的值,并證明:對任意的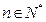 ,
,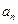 是
是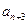 與
與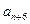 的等差中項;
的等差中項; 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案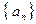 的前
的前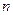 項和為
項和為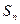 ,
,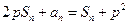
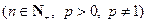 ,數(shù)列
,數(shù)列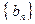 滿足
滿足 .(Ⅰ)求數(shù)列
.(Ⅰ)求數(shù)列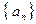 和
和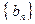 的通項公式; (Ⅱ)當
的通項公式; (Ⅱ)當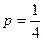 時,
時,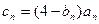 ,求數(shù)列
,求數(shù)列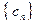 的前
的前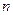 項和
項和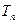 .
.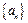 的前n項的和Sn,滿足
的前n項的和Sn,滿足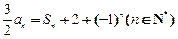 .
.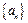 的通項公式.(2)設(shè)
的通項公式.(2)設(shè)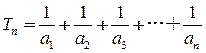 ,是否存在正整數(shù)k,使得當n≥3時,
,是否存在正整數(shù)k,使得當n≥3時,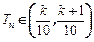 如果存在,求出k;如果不存在,請說明理由.
如果存在,求出k;如果不存在,請說明理由. 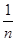 ),f(
),f(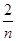 ),
),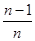 )……,(n≥2,n∈
)……,(n≥2,n∈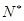 )的前n項的和為Sn ;
)的前n項的和為Sn ;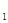 =
=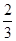 ,a
,a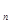 =" "
=" " 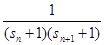 (n≥2,n∈
(n≥2,n∈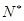 ),
),