
某人進(jìn)行了如下的“三段論”推理:
如果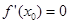 ,則
,則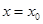 是函數(shù)
是函數(shù)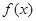 的極值點(diǎn),因?yàn)楹瘮?shù)
的極值點(diǎn),因?yàn)楹瘮?shù)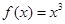 在
在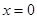 處的導(dǎo)數(shù)值
處的導(dǎo)數(shù)值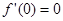 ,所以
,所以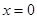 是函數(shù)
是函數(shù)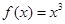 的極值點(diǎn)。你認(rèn)為以上推理的
的極值點(diǎn)。你認(rèn)為以上推理的
| A.大前提錯(cuò)誤 | B.小前提錯(cuò)誤 | C.推理形式錯(cuò)誤 | D.結(jié)論正確 |
A
解析試題分析:解:∵大前提是:“對于可導(dǎo)函數(shù)f(x),如果f'(x0)=0,那么x=x0是函數(shù)f(x)的極值點(diǎn)”,不是真命題,因?yàn)閷τ诳蓪?dǎo)函數(shù)f(x),如果f'(x0)=0,且滿足當(dāng)x>x0時(shí)和當(dāng)x<x0時(shí)的導(dǎo)函數(shù)值異號時(shí),那么x=x0是函數(shù)f(x)的極值點(diǎn),∴大前提錯(cuò)誤,故選A.
考點(diǎn):演繹推理
點(diǎn)評:本題考查的知識點(diǎn)是演繹推理的基本方法,演繹推理是一種必然性推理,演繹推理的前提與結(jié)論之間有蘊(yùn)涵關(guān)系.因而,只要前提是真實(shí)的,推理的形式是正確的,那么結(jié)論必定是真實(shí)的,但錯(cuò)誤的前提可能導(dǎo)致錯(cuò)誤的結(jié)論.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
用反證法證明命題:若整數(shù)系數(shù)的一元二次方程 有有理實(shí)數(shù)根,那么
有有理實(shí)數(shù)根,那么 ,
, ,
, 中至少有一個(gè)是偶數(shù),下列假設(shè)中正確的是( )
中至少有一個(gè)是偶數(shù),下列假設(shè)中正確的是( )
A.假設(shè) , , , , 都是偶數(shù) 都是偶數(shù) |
B.假設(shè) , , , , 都不是偶數(shù) 都不是偶數(shù) |
C.假設(shè) , , , , 至多有一個(gè)是偶數(shù) 至多有一個(gè)是偶數(shù) |
D.假設(shè) , , , , 至多有兩個(gè)偶數(shù) 至多有兩個(gè)偶數(shù) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用反證法證明命題:“一個(gè)三角形中不能有兩個(gè)直角”的過程歸納為以下三個(gè)步驟:
① ,這與三角形內(nèi)角和為
,這與三角形內(nèi)角和為 相矛盾,
相矛盾, 不成立;②所以一個(gè)三角形中不能有兩個(gè)直角;③假設(shè)三角形的三個(gè)內(nèi)角
不成立;②所以一個(gè)三角形中不能有兩個(gè)直角;③假設(shè)三角形的三個(gè)內(nèi)角 、
、 、
、 中有兩個(gè)直角,不妨設(shè)
中有兩個(gè)直角,不妨設(shè) ,正確順序的序號為
,正確順序的序號為
| A.①②③ | B.③①② | C.①③② | D.②③① |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用反證法證明命題“三角形的內(nèi)角中至少有一個(gè)角不大于 ”時(shí),反設(shè)正確的是
”時(shí),反設(shè)正確的是
A.假設(shè)三個(gè)內(nèi)角都不大于 | B.假設(shè)三個(gè)內(nèi)角都大于 |
C.假設(shè)三個(gè)內(nèi)角至多有一個(gè)大于 | D.假設(shè)三個(gè)內(nèi)角至多有二個(gè)大于 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
下列三句話按三段論的模式排列順序正確的是( )
① 2013不能被2整除; ② 一切奇數(shù)都不能被2整除; ③ 2013是奇數(shù);
| A.①②③ | B.②①③ | C.②③① | D.③②① |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在平面上,若兩個(gè)正三角形的邊長比為1:2.則它們的面積之比為1:4.類似地,在空間中,若兩個(gè)正四面體的棱長比為1:2,則它們的體積比為( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
觀察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
…
照此規(guī)律,第n個(gè)等式為 _________ .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
設(shè) 表示不超過
表示不超過 的最大整數(shù),如
的最大整數(shù),如 .我們發(fā)現(xiàn):
.我們發(fā)現(xiàn): ;
; ;
; ;
;
.......
通過合情推理,寫出一般性的結(jié)論 (用含 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
用數(shù)學(xué)歸納法證明“n3+(n+1)3+(n+2)3,(n∈N+)能被9整除”,要利
用歸納法假設(shè)證n=k+1時(shí)的情況,只需展開( ).
| A.(k+3)3 | B.(k+2)3 |
| C.(k+1)3 | D.(k+1)3+(k+2)3 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com