
對于三次函數(shù)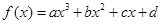 (
(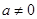 ),定義:設(shè)f″(x)是函數(shù)y=f′(x)的導(dǎo)數(shù),若方程f″(x)=0有實數(shù)解x0,則稱點(x0,f(x0))為函數(shù)
),定義:設(shè)f″(x)是函數(shù)y=f′(x)的導(dǎo)數(shù),若方程f″(x)=0有實數(shù)解x0,則稱點(x0,f(x0))為函數(shù) 的“拐點”.有同學(xué)發(fā)現(xiàn):“任何一個三次函數(shù)都有‘拐點’;任何一個三次函數(shù)都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發(fā)現(xiàn)為條件,若函數(shù)
的“拐點”.有同學(xué)發(fā)現(xiàn):“任何一個三次函數(shù)都有‘拐點’;任何一個三次函數(shù)都有對稱中心;且‘拐點’就是對稱中心.”請你將這一發(fā)現(xiàn)為條件,若函數(shù)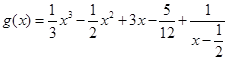 ,則
,則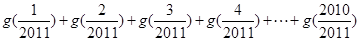 =( )
=( )
| A.2010 | B.2011 | C.2012 | D.2013 |
A
解析試題分析:因為函數(shù)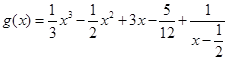 =
=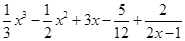 ,
,
所以令h(x)= ,m(x)=
,m(x)=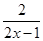 ,則g(x)=h(x)+m(x).
,則g(x)=h(x)+m(x).
則h′(x)=x2-x+3,h″(x)=2x-1,令h″(x)=0,可得x= ,故h(x)的對稱中心為(
,故h(x)的對稱中心為( ,1).
,1).
設(shè)點p(x0,y0)為曲線上任意一點,則點P關(guān)于( ,1)的對稱點P′(1-x0,2-y0)也在曲線上,∴h(1-x0)=2-y0 ,∴h(x0)+h(1-x0)=y0+(2-y0)=2.
,1)的對稱點P′(1-x0,2-y0)也在曲線上,∴h(1-x0)=2-y0 ,∴h(x0)+h(1-x0)=y0+(2-y0)=2.
所以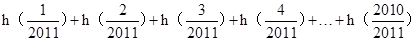
=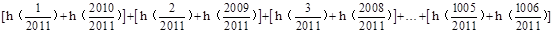 =1005×2=2010.
=1005×2=2010.
由于函數(shù)m(x)=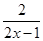 的對稱中心為(
的對稱中心為( ,0),可得m(x0)+m(1-x0)=0.
,0),可得m(x0)+m(1-x0)=0.
∴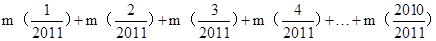
=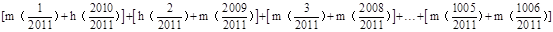 =1005×0=0.
=1005×0=0.
所以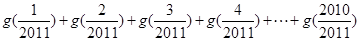 =
=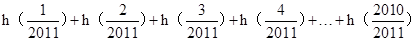 +
+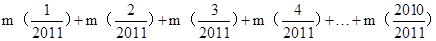
=2010+0=2010,故答案為2010.
考點:本題主要考查函數(shù)的概念,函數(shù)圖象的對稱性,導(dǎo)數(shù)的計算。
點評:難題,運用化歸與轉(zhuǎn)化的數(shù)學(xué)思想方法,將函數(shù)g(x)的研究進(jìn)行拆分,簡化了解題過程。解答此類題目,心理素質(zhì)首先要過關(guān),不畏難,靜心思考。


科目:高中數(shù)學(xué) 來源: 題型:單選題
已知R上的不間斷函數(shù)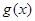 滿足:①當(dāng)
滿足:①當(dāng)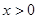 時,
時, 恒成立;②對任意的
恒成立;②對任意的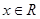 都有
都有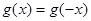 。又函數(shù)
。又函數(shù)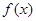 滿足:對任意的
滿足:對任意的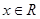 ,都有
,都有 成立,當(dāng)
成立,當(dāng) 時,
時, 。若關(guān)于
。若關(guān)于 的不等式
的不等式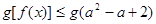 對
對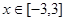 恒成立,則
恒成立,則 的取值范圍( )
的取值范圍( )
A.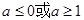 | B.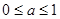 | C.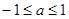 | D.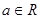 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com