已知函數f（x）=
，x∈[1，3]，
（1）求f（x）的最大值與最小值；
（2）若
于任意的x∈[1，3]，t∈[0，2]恒成立，求實數a的取值范圍．
（1）
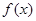的最大值為
，最小值為
；（2）
.
解析試題分析：（1）先求導函數
，再求
的根，再判斷根兩側導數的符號，進而判斷函數大致圖象，再從大致圖象并比較端點函數值的大小來確定最大值和最小值；（2）恒成立問題關鍵搞清變量和參數的關系，一般遵循“知道誰的范圍，誰是變量；求誰的范圍，誰是參數”的原則，該題中首先利用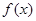的最大值小于
，得關于
恒成立的不等式，再根據
，求參數
的范圍.
試題解析：（1）因為函數
，所以
，令
得
，因為
，
當
時 
；當
時，
；∴
在
上單調減函數，在
上單調增函數，∴在
處取得極小值
； 又
，
，∵
∴
∴
，
∴
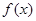時的最大值為，
時函數取得最小值為．
（2）由（1）知當
時，
，故對任意，恒成立，
只要
對任意恒成立，即
恒成立，記
，
∴
，解得
，∴實數a的取值范圍是．
考點：1、導數在單調性上的應用；2、利用導數求函數的極值和最值.
雙基同步導航訓練系列答案
黃岡小狀元同步計算天天練系列答案科目：高中數學 來源： 題型：解答題
已知函數
為奇函數.
（1）求常數
的值；
（2）判斷函數的單調性，并說明理由；
（3）函數
的圖象由函數
的圖象先向右平移2個單位，再向上平移2個單位得到，寫出的一個對稱中心，若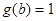
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝log4(4x＋1)＋kx(k∈R)是偶函數．
(1)求k的值；
(2)探究函數f(x)＝ax＋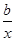
(a、b是正常數)在區間
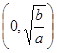和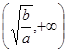
上的單調性（只需寫出結論，不要求證明）.并利用所得結論，求使方程f(x)－log4m＝0有解的m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
運貨卡車以每小時x千米的勻速行駛130千米，按交通法規限制50≤x≤100（單位：千米／小時）.假設汽油的價格是每升2元，而汽車每小時耗油（
）升，司機的工資是每小時14元.
（1）求這次行車總費用y關于x的表達式；
（2）當x為何值時，這次行車的總費用最低，并求出最低費用的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
f(2x)
在
上為減函數。
上的最小值.
和
的圖像關于原點對稱，且
．
；
在區間
上是增函數，求實數
的取值范圍．
（
）
的定義域；
、
，當
時，
，且
若存在，求出
,函數
且
，
且
.
滿足
且
，函數
是否具有奇偶性? 如果有,求出相應的
值;如果沒有,說明原因；
，討論函數
，
且
.
的值;
在
的單調性，并用定義加以證明.