
已知 是關于
是關于 的方程
的方程 的兩個根.
的兩個根.
(1)求 的值;
的值;
(2)求 的值.
的值.
(1) ;(2)
;(2)  .
.
解析試題分析:先利用一元二次方程根的判別式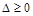 ,得
,得 或
或 ,結合已知條件、韋達定理及平方關系
,結合已知條件、韋達定理及平方關系 ,可得
,可得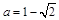 ,從而由韋達定理得
,從而由韋達定理得
(1) 利用誘導公式將欲求式化簡,得 ,代入即可求其值;
,代入即可求其值;
(2) 利用誘導公式三角函數基本關系式將欲求式化簡成: 代入即可求其值.
代入即可求其值.
試題解析:由已知原方程判別式Δ≥0,即 或
或 ,又
,又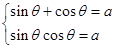
∴(sin θ+cos θ)2=1+2sin θcos θ,即a2-2a-1=0.
∴a=1-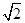 或a=1+
或a=1+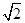 (舍去).∴sin θ+cos θ=sin θcos θ=1-
(舍去).∴sin θ+cos θ=sin θcos θ=1-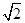 .
.
(1) ="-(sin" θ+cos θ)=
="-(sin" θ+cos θ)=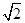 -1
-1
(2)tan(π-θ)-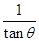 =-tan θ-
=-tan θ-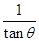
=-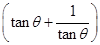 =-
=-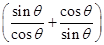 =-
=- =-
=- =
=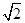 +1.
+1.
考點:1.韋達定理;2.三角函數求值.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
如圖所示,扇形AOB,圓心角AOB的大小等于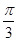 ,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
(1)若C是半徑OA的中點,求線段PC的長;
(2)設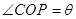 ,求
,求 面積的最大值及此時
面積的最大值及此時 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
定義在區間 上的函數
上的函數 的圖象關于直線
的圖象關于直線 對稱,當
對稱,當 時函數
時函數 圖象如圖所示
圖象如圖所示
(Ⅰ)求函數 在
在 的表達式;
的表達式;
(Ⅱ)求方程 的解;
的解;
(Ⅲ)是否存在常數 的值,使得
的值,使得 在
在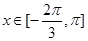 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范圍;若不存在,請說明理由
的取值范圍;若不存在,請說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com