
如圖,在等腰直角三角形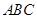 中,
中, 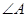 =900 ,
=900 ,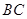 ="6,"
="6," 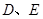 分別是
分別是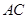 ,
,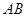 上的點(diǎn),
上的點(diǎn),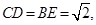
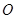 為
為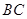 的中點(diǎn).將
的中點(diǎn).將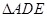 沿
沿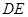 折起,得到如圖所示的四棱椎
折起,得到如圖所示的四棱椎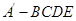 ,其中
,其中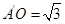
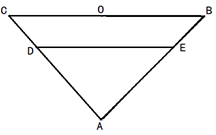
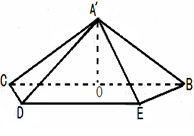
(1)證明: ;
;
(2)求二面角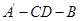 的平面角的余弦值.
的平面角的余弦值.
(1)詳見解析 (2)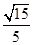
解析試題分析:(1)F為ED的中點(diǎn),連接OF,A’F,根據(jù)已知計算出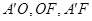 的長度,滿足勾股定理,
的長度,滿足勾股定理,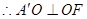 , A’F為等腰△A’DE底邊的中線,
, A’F為等腰△A’DE底邊的中線,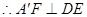 ,
,  ,證得線面垂直,線線垂直,再線面垂直;(2)過點(diǎn)O作
,證得線面垂直,線線垂直,再線面垂直;(2)過點(diǎn)O作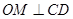 的延長線于
的延長線于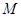 ,連接
,連接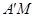 .利用(1)可知:
.利用(1)可知: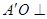 平面
平面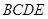 ,根據(jù)三垂線定理得
,根據(jù)三垂線定理得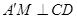 ,所以
,所以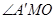 為二面角
為二面角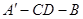 的平面角.在直角
的平面角.在直角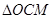 中,求出
中,求出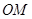 即可;
即可;
試題解析:
證明: (1)設(shè)F為ED的中點(diǎn),連接OF,A’F,計算得A’F=2,OF=1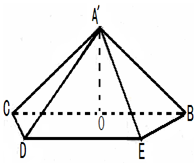
∵A’F為等腰△A’DE底邊的中線,∴A’F⊥DE
∵OF在原等腰△ABC底邊BC的高線上,
∴OF⊥DE
又∵A’F,OF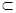 平面A’OF, A’F
平面A’OF, A’F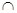 OF=F,
OF=F,
∴DE⊥平面A’OF
∵A’O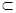 平面A’OF, ∴DE⊥A’O
平面A’OF, ∴DE⊥A’O
在△A’FO中,A’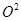 +
+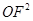 =3+1=
=3+1=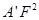 ,∴A’O⊥OF
,∴A’O⊥OF
∵OF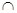 DE=F,OF
DE=F,OF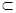 平面BCDE,DE
平面BCDE,DE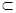 平面BCDE, ∴A’O⊥平面BCDE 6分
平面BCDE, ∴A’O⊥平面BCDE 6分
(2):如答圖1,過O作CD的垂線交CD的延長線于M,連接A’M
∵A’O⊥平面BCDE,CD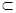 平面BCDE, ∴CD⊥A’O ∵OM
平面BCDE, ∴CD⊥A’O ∵OM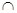 A’O="O," ∴CD⊥平面A’OM
A’O="O," ∴CD⊥平面A’OM
∵A’M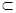 平面A’OM∴CD⊥A’M ∴
平面A’OM∴CD⊥A’M ∴ ∠A’MO為所求二面角的平面角
∠A’MO為所求二面角的平面角
在Rt△OMC中,OM=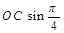 =
=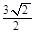 , A’O=
, A’O=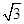 于是在Rt△A’OM中,A’M=
于是在Rt△A’OM中,A’M=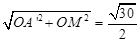 ∴
∴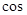 ∠A’OM=
∠A’OM=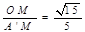 13分
13分
考點(diǎn):1.線面垂直的判定;2.二面角的定義.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
定理:如果一條直線和一個平面平行,經(jīng)過這條直線的平面和這個平面相交,那么這條直線就和兩平面的交線平行.
請對上面定理加以證明,并說出定理的名稱及作用.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知四棱錐P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD= AB.Q是PC上的一點(diǎn).
AB.Q是PC上的一點(diǎn).
⑴求證:平面PAD⊥面PBD;
⑵當(dāng)Q在什么位置時,PA∥平面QBD?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,三棱柱 的底面是邊長為2的正三角形,且側(cè)棱垂直于底面,側(cè)棱長是,D是AC的中點(diǎn)。
的底面是邊長為2的正三角形,且側(cè)棱垂直于底面,側(cè)棱長是,D是AC的中點(diǎn)。
(1)求證: 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)求直線 與平面
與平面 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,四棱錐P ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分別為PB,AB,BC,PD,PC的中點(diǎn)
ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分別為PB,AB,BC,PD,PC的中點(diǎn)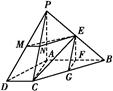
(1)求證:CE∥平面PAD;
(2)求證:平面EFG⊥平面EMN.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在直三棱柱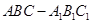 中,D、E分別是BC和
中,D、E分別是BC和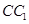 的中點(diǎn),已知AB=AC=AA1=4,ÐBAC=90°.
的中點(diǎn),已知AB=AC=AA1=4,ÐBAC=90°.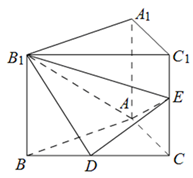
(1)求證: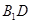 ⊥平面
⊥平面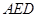 ;
;
(2)求二面角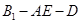 的余弦值;
的余弦值;
(3)求三棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖①,E、F分別是直角三角形ABC邊AB和AC的中點(diǎn),∠B=90°,沿EF將三角形ABC折成如圖②所示的銳二面角A1EFB,若M為線段A1C中點(diǎn).求證: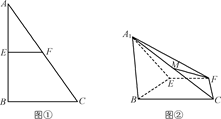
(1)直線FM∥平面A1EB;
(2)平面A1FC⊥平面A1BC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
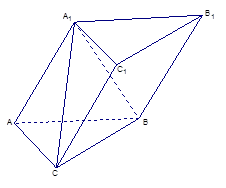
如圖,棱柱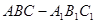 中,四邊形
中,四邊形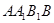 是菱形,四邊形
是菱形,四邊形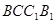 是矩形,
是矩形,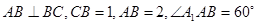 .
.
(1)求證:平面 ;
;
(2)求點(diǎn)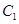 到平面
到平面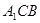 的距離;
的距離;
(3)求直線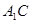 與平面
與平面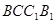 所成角的正切值.
所成角的正切值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com