Question

求由直線x=1,x=2,y=0及曲線y=圍成的圖形的面積S.

Answer 1

分析:利用求曲邊梯形面積的步驟逐步求解.

解:(1)分割

在區間［1,2］內等間隔地插入n-1個點,將它等分成n個小區間：［1,］,［,］,…,［,2］,記第i個區間為［］(i=1,2,…,n)，其長度為Δx=

分別過上述n-1個點作x軸的垂線,把曲邊梯形分成n個小曲邊梯形(如下圖)，它們的面積記作ΔS₁,ΔS₂,…,ΔS_n.

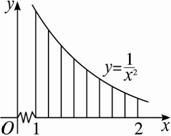
則小曲邊梯形面積的和為S=.

(2)近似代替

記f(x)=,當n很大，即Δx很小時，在區間上，可以認為f(x)=的值變化很小，近似地等于一個常數,不妨認為它等于.從圖形上看，就是用平行于x軸的直線段近似地代替小曲邊梯形的曲邊.這樣,在區間上，用小矩形面積ΔS_i′近似地代替ΔS_i，即在局部小范圍內“以直代曲”，則有ΔS_i≈ΔS_i′=f(i=1,2,…,n).

(3)求和

小曲邊梯形的面積和S_n=

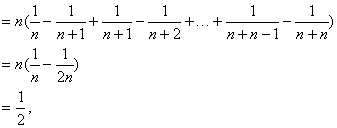
從而得到S的近似值S=S_n≈

(4)取極限

分別將區間［1,2］等分成8,16,20,…等份時,S_n越來越趨向于S,當n趨向于+∞時,S_n無限趨近于.

由此可知圖形面積為.

綠色通道:本題主要考查曲邊梯形面積的求解方法.用分割、近似代替、求和、取極限這四個步驟可以求曲邊多邊形的面積,它體現了一種化整(分割)為零,積零為整(逼近)的思想方法.