
已知函數 (a,b均為正常數).
(a,b均為正常數).
(1)求證:函數 在
在 內至少有一個零點;
內至少有一個零點;
(2)設函數在 處有極值,
處有極值,
①對于一切 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范圍;
的取值范圍;
②若函數f(x)在區間 上是單調增函數,求實數
上是單調增函數,求實數 的取值范圍.
的取值范圍.
(1)詳見解析;(Ⅱ)① ②
②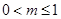 .
.
解析試題分析:(Ⅰ)證明函數 在
在 內至少有一個零點,可由零點的存在性定理考察
內至少有一個零點,可由零點的存在性定理考察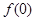 和
和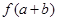 的符號,若
的符號,若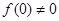 且
且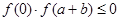 ,則結論成立,若
,則結論成立,若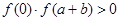 ,可將區間
,可將區間 進行適當分割,再依上面方法進行,直到找到函數的零點的存在區間;(Ⅱ)易知
進行適當分割,再依上面方法進行,直到找到函數的零點的存在區間;(Ⅱ)易知 ,從而求出
,從而求出 的值.
的值.
①不等式 恒成立可化分離參數轉化為求函數在區間
恒成立可化分離參數轉化為求函數在區間 上的最值問題,這是一個普通的三角函數問題,通過判斷三角函數的單調性容易解決;②函數在一個已知區間上為增函數,求參數的取值范圍問題,通常有兩種方法,一是用在這個區間上導函數的符號確定,一般三角函數不用此方法,二是求出函數的單調遞增區間,它必包含已知區間,然后考察參數的取值范圍.
上的最值問題,這是一個普通的三角函數問題,通過判斷三角函數的單調性容易解決;②函數在一個已知區間上為增函數,求參數的取值范圍問題,通常有兩種方法,一是用在這個區間上導函數的符號確定,一般三角函數不用此方法,二是求出函數的單調遞增區間,它必包含已知區間,然后考察參數的取值范圍.
試題解析:(1)證明: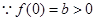 ,
,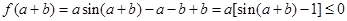

所以,函數 在
在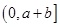 內至少有一個零點 4分
內至少有一個零點 4分
(2)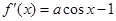 由已知得:
由已知得: 所以a=2,
所以a=2,
所以 5分
5分
①不等式 恒成立可化為:
恒成立可化為: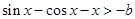
記函數

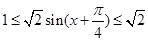 ,所以
,所以 在
在 恒成立 8分
恒成立 8分
函數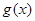 在
在 上是增函數,最小值為
上是增函數,最小值為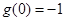
所以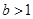 , 所以
, 所以 的取值范圍是
的取值范圍是 10分
10分
②由 得:
得: ,所以
,所以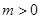 11分
11分
令 ,可得
,可得 13分
13分
∵函數 在區間(
在區間(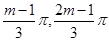 )上是單調增函數,
)上是單調增函數,
∴ 14分
14分
∴ ,
,
∵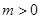 ,∴
,∴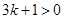 ,
,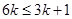 ∴
∴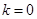 ∴
∴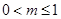 16分
16分
考點:函數的零點、三角函數的性質.


 名校課堂系列答案
名校課堂系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com