
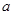 ∈R,函數
∈R,函數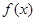 =
=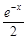 (
(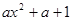 ),其中e是自然對數的底數.
),其中e是自然對數的底數.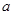 < 0時,求f (x)在[1,2]上的最小值.
< 0時,求f (x)在[1,2]上的最小值.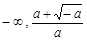 )上, f (x)單調遞增;在區間(
)上, f (x)單調遞增;在區間(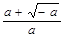 ,
,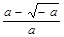 )上, f (x)單調遞減;在區間(
)上, f (x)單調遞減;在區間(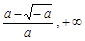 )上, f (x)單調遞增.
)上, f (x)單調遞增. 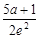
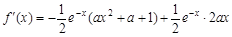 =
=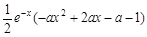 . ……2 分
. ……2 分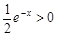 ,以下討論函數g (x) = –a
,以下討論函數g (x) = –a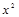 + 2ax – a – 1值的情況.
+ 2ax – a – 1值的情況.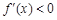 ,所以f (x)在R上是減函數. ……3分
,所以f (x)在R上是減函數. ……3分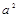 – 4(
– 4(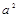 +a) =" –4a" < 0,
+a) =" –4a" < 0,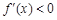 ,所以f(x)在R上是減函數. ……5分
,所以f(x)在R上是減函數. ……5分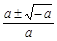 ,并且
,并且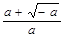 <
<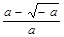 ,
,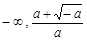 )上,g (x) > 0,即
)上,g (x) > 0,即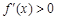 ,f (x)在此區間上 是增函數.
,f (x)在此區間上 是增函數.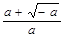 ,
,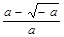 )上,g (x) < 0,即
)上,g (x) < 0,即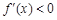 ,f (x)在此區間上是減函數.
,f (x)在此區間上是減函數.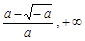 )上,g (x) > 0,即
)上,g (x) > 0,即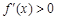 ,f (x)在此區間上是增函數. ……7分
,f (x)在此區間上是增函數. ……7分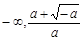 )上單調遞增,在(
)上單調遞增,在(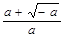 ,
,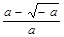 )上單調遞減,在(
)上單調遞減,在(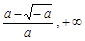 )上單調遞增. ……8分
)上單調遞增. ……8分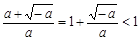 ,
,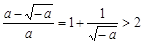 , ……10分
, ……10分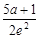 . ……12分
. ……12分

 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案科目:高中數學 來源:不詳 題型:單選題
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com