
設函數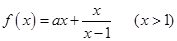
(1)若a>0,求函數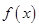 的最小值;
的最小值;
(2)若a是從1,2,3三個數中任取一個數,b是從2,3,4,5四個數中任取一個數,求f (x)>b恒成立的概率。
(1) 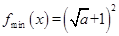 (2)
(2) 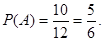
解析試題分析: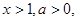
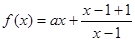
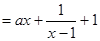
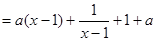
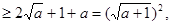
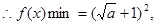
于是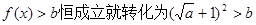 成立。
成立。
設事件A:“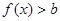 恒成立”,則
恒成立”,則
基本事件總數為12個,即
(1,2),(1,3),(1,4),(1,5);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5);
事件A包含事件:(1,2),(1,3);
(2,2),(2,3),(2,4),(2,5);
(3,2),(3,3),(3,4),(3,5)共10個
由古典概型得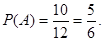
考點:基本不等式;古典概型。
點評:本題考查用列舉法計算基本事件數及隨機事件發生的概率,解題的關鍵是熟練運用分類列舉的方法及事件的性質將所有的基本事件一一列舉出來,運用公式求出概率,注意列舉時要不重不漏。列舉法求概率適合基本事件數不太多的概率求解問題。


科目:高中數學 來源: 題型:解答題
(12分)已知函數 .
.
(1)若曲線 在點
在點 處的切線與直線
處的切線與直線 垂直,求函數
垂直,求函數 的單調區間;
的單調區間;
(2)若對于 都有
都有 成立,試求
成立,試求 的取值范圍;
的取值范圍;
(3)記 .當
.當 時,函數
時,函數 在區間
在區間 上有兩個零點,求實數
上有兩個零點,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分16分)
已知函數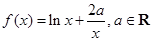 .
.
(1)若x=2是函數f(x)的極值點,求實數a的值.
(2)若函數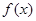 在
在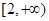 上是增函數,求實數
上是增函數,求實數 的取值范圍;
的取值范圍;
(3)若函數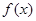 在
在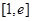 上的最小值為3,求實數
上的最小值為3,求實數 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com