
(本小題滿分12分)已知函數(shù) .
.
(Ⅰ)設(shè) ,討論
,討論 的單調(diào)性;
的單調(diào)性;
(Ⅱ)若對任意 恒有
恒有 ,求
,求 的取值范圍.
的取值范圍.
解:(1) 解析
科目:高中數(shù)學(xué)
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學(xué)
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學(xué)
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學(xué)
來源:
題型:解答題
設(shè)
科目:高中數(shù)學(xué)
來源:
題型:解答題
(本小題滿分14分)設(shè)函數(shù)
科目:高中數(shù)學(xué)
來源:
題型:解答題
已知定義在R上的函數(shù)
科目:高中數(shù)學(xué)
來源:
題型:解答題
(本小題滿分10分)為了在夏季降溫和冬季供暖時(shí)減少能源損耗,房屋的屋頂和
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表 湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū) 的定義域?yàn)椋?sub>
的定義域?yàn)椋?sub> ,1)
,1) (1,
(1, )
)

因?yàn)?sub> (其中
(其中 )恒成立,所以
)恒成立,所以 .…………………2分
.…………………2分
當(dāng) 時(shí),
時(shí), 在(
在( ,0)
,0) (1,
(1, )上恒成立,所以
)上恒成立,所以 在(
在( ,1)
,1) (1,
(1, )上為增函數(shù); …………………………………4分
)上為增函數(shù); …………………………………4分
當(dāng) 時(shí),
時(shí), 在(
在( ,0)
,0) (0,1)
(0,1) (1,
(1, )上恒成立,所以
)上恒成立,所以 在(
在( ,1)
,1) (1,
(1, )上為增函數(shù);……………………………
)上為增函數(shù);…………………………… ……6分
……6分
當(dāng) 時(shí),
時(shí), 的解為:(
的解為:( ,
,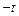 )
) (t,1)
(t,1) (1,+
(1,+ )
)
(其中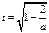 ).
).
所以 在各區(qū)間內(nèi)的增減性如下表:
在各區(qū)間內(nèi)的增減性如下表:區(qū)間 (  ,
,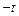 )
)( 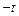 ,t)
,t)(t,1) (1,+  )
) 的符號(hào)
的符號(hào)+ 
+ +  的單調(diào)性
的單調(diào)性增函數(shù)


西城學(xué)科專項(xiàng)測試系列答案
小考必做系列答案
小考實(shí)戰(zhàn)系列答案
小考復(fù)習(xí)精要系列答案
小考總動(dòng)員系列答案
小升初必備沖刺48天系列答案
68所名校圖書小升初高分奪冠真卷系列答案
伴你成長周周練月月測系列答案
小升初金卷導(dǎo)練系列答案
萌齊小升初強(qiáng)化模擬訓(xùn)練系列答案

年級(jí)
高中課程
年級(jí)
初中課程
高一
高一免費(fèi)課程推薦!
初一
初一免費(fèi)課程推薦!
高二
高二免費(fèi)課程推薦!
初二
初二免費(fèi)課程推薦!
高三
高三免費(fèi)課程推薦!
初三
初三免費(fèi)課程推薦!
 ,且其導(dǎo)函數(shù)
,且其導(dǎo)函數(shù)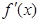 的圖像過原點(diǎn).
的圖像過原點(diǎn).
(1)當(dāng) 時(shí),求函數(shù)
時(shí),求函數(shù) 的圖像在
的圖像在 處的切線方程;
處的切線方程;
(2)若存在 ,使得
,使得 ,求
,求 的最大值;
的最大值; 定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/2f/d/f4d492.gif" style="vertical-align:middle;" />(
定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/2f/d/f4d492.gif" style="vertical-align:middle;" />( ),設(shè)
),設(shè) .
.
(1)試確定 的取值范圍,使得函數(shù)
的取值范圍,使得函數(shù) 在
在 上為單調(diào)函數(shù);
上為單調(diào)函數(shù);
(2)求證: ;
;
(3)求證:對于任意的 ,總存在
,總存在 ,滿足
,滿足 ,并確定這樣的
,并確定這樣的 的個(gè)數(shù).
的個(gè)數(shù). 。
。
(1)若 ,求函數(shù)
,求函數(shù) 在
在 上的最小值;
上的最小值;
(2)若函數(shù) 在
在 上存在單調(diào)遞增區(qū)間,試求實(shí)數(shù)
上存在單調(diào)遞增區(qū)間,試求實(shí)數(shù) 的取值范圍。
的取值范圍。 .
.
(1)若 在
在 上存在單調(diào)遞增區(qū)間,求
上存在單調(diào)遞增區(qū)間,求 的取值范圍;
的取值范圍;
(2)當(dāng) 時(shí),
時(shí), 在
在 上的最小值為
上的最小值為 ,求
,求 在該區(qū)間上
在該區(qū)間上
的最大值. ,
, .
.
(Ⅰ)當(dāng) 時(shí),
時(shí), 在
在 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)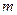 的取值范圍;
的取值范圍;
(Ⅱ)當(dāng) 時(shí),若函數(shù)
時(shí),若函數(shù) 在
在 上恰有兩個(gè)不同零點(diǎn),求實(shí)數(shù)
上恰有兩個(gè)不同零點(diǎn),求實(shí)數(shù) 的取值
的取值 范圍;
范圍;
(Ⅲ)是否存在實(shí)數(shù)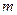 ,使函數(shù)
,使函數(shù) 和函數(shù)
和函數(shù) 在公共定義域上具有相同的單調(diào)性?若存在,求出
在公共定義域上具有相同的單調(diào)性?若存在,求出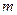 的值,若不存在,說明理由.
的值,若不存在,說明理由. ,其中a為常數(shù).
,其中a為常數(shù).
(I)若x=1是函數(shù) 的一個(gè)極值點(diǎn),求a的值;
的一個(gè)極值點(diǎn),求a的值;
(II)若函數(shù) 在區(qū)間(-1,0)上是增函數(shù),求a的取值范圍;
在區(qū)間(-1,0)上是增函數(shù),求a的取值范圍;
(III)若函數(shù) ,在x=0處取得最大值,求正數(shù)a的取值范圍.
,在x=0處取得最大值,求正數(shù)a的取值范圍.
外墻需要建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成
本為6萬元.該建筑物每年的能源消耗費(fèi)用C(單位:萬 元)與隔熱層厚度x(單位:cm)
元)與隔熱層厚度x(單位:cm)
滿足兩個(gè)關(guān)系:①C(x)= ②若不建隔熱層,每年能源消耗費(fèi)用為8萬
②若不建隔熱層,每年能源消耗費(fèi)用為8萬
元。設(shè)f(x)為隔熱層建造費(fèi)用與20年的能源消耗費(fèi)用之和.
(Ⅰ)求k的值及f(x)的表達(dá)式; (4分)
(Ⅱ)隔熱層修建多厚時(shí),總費(fèi)用f(x)達(dá)到最小,并求最小值.
版權(quán)聲明:本站所有文章,圖片來源于網(wǎng)絡(luò),著作權(quán)及版權(quán)歸原作者所有,轉(zhuǎn)載無意侵犯版權(quán),如有侵權(quán),請作者速來函告知,我們將盡快處理,聯(lián)系qq:3310059649。
ICP備案序號(hào): 滬ICP備07509807號(hào)-10 鄂公網(wǎng)安備42018502000812號(hào)