
已知函數
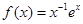 的定義域為
的定義域為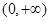 .
.
(I)求函數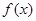 在
在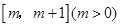 上的最小值;
上的最小值;
(Ⅱ)對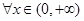 ,不等式
,不等式 恒成立,求
恒成立,求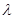 的取值范圍.
的取值范圍.
(1)當 時,
時,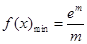 ,當
,當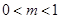 時,
時,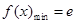 ;(2)
;(2)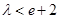 .
.
解析試題分析:(I)先用導數工具求出函數在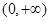 上的單調區間,然后考察區間
上的單調區間,然后考察區間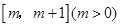 與其關系,根據需要對
與其關系,根據需要對 分類討論;(Ⅱ)不等式恒成立問題,通常可以通過分離參數轉化為求函數的最值問題,如本題分離參數后可得到,
分類討論;(Ⅱ)不等式恒成立問題,通常可以通過分離參數轉化為求函數的最值問題,如本題分離參數后可得到, ,然后轉化為求左邊函數的最小值問題,可用導數判斷其單調性,再求出最小值,
,然后轉化為求左邊函數的最小值問題,可用導數判斷其單調性,再求出最小值,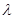 小于這個最小值即可.對于不等式恒成立問題通常可以通過分離參數或直接考察函數的性質解決,一般來說方便分離參數的還是分離參數,這樣在研究函數的性質時可避開參變數的影響,便于解決問題.
小于這個最小值即可.對于不等式恒成立問題通常可以通過分離參數或直接考察函數的性質解決,一般來說方便分離參數的還是分離參數,這樣在研究函數的性質時可避開參變數的影響,便于解決問題.
試題解析:解: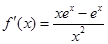 , 1分
, 1分
令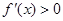 得
得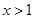 ;令
;令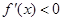 得
得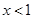
所以,函數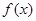 在
在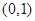 上是減函數;在
上是減函數;在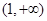 上是增函數 3分
上是增函數 3分
(I)當 時,函數
時,函數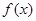 在
在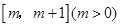 上是增函數,
上是增函數,
所以, 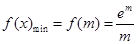 5分
5分
當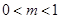 時,函數
時,函數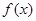 在
在 上是減函數;在
上是減函數;在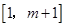 上是增函數
上是增函數
所以,  7分
7分
(Ⅱ)由題意,對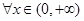 ,不等式
,不等式 恒成立
恒成立
即  恒成立 9分
恒成立 9分
令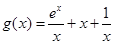 ,則
,則 11分
11分
由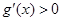 得
得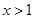 ;由
;由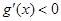 得
得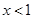 13分
13分
所以,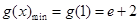 。 所以,
。 所以,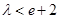 . 14分
. 14分
考點:函數與導數、函數的極值和最值.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:解答題
設函數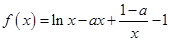 .
.
(1)當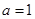 時,求曲線
時,求曲線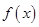 在
在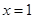 處的切線方程;
處的切線方程;
(2)當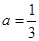 時,求函數
時,求函數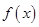 的單調區間;
的單調區間;
(3)在(2)的條件下,設函數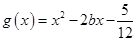 ,若對于
,若對于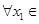 [1,2],
[1,2],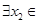 [0,1],使
[0,1],使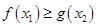 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com