
已知函數(shù) 的導函數(shù)是
的導函數(shù)是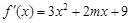 ,
, 在
在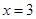 處取得極值,且
處取得極值,且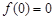 .
.
(Ⅰ)求 的極大值和極小值;
的極大值和極小值;
(Ⅱ)記 在閉區(qū)間
在閉區(qū)間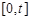 上的最大值為
上的最大值為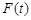 ,若對任意的
,若對任意的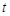
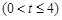 總有
總有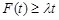 成立,求
成立,求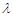 的取值范圍;
的取值范圍;
(Ⅲ)設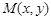 是曲線
是曲線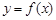 上的任意一點.當
上的任意一點.當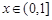 時,求直線OM斜率的最小值,據(jù)此判斷
時,求直線OM斜率的最小值,據(jù)此判斷 與
與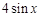 的大小關系,并說明理由.
的大小關系,并說明理由.
(Ⅰ) 的極大值為
的極大值為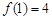 ,極小值為
,極小值為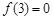 ;(Ⅱ)
;(Ⅱ)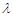 的取值范圍是:
的取值范圍是: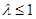 ;(Ⅲ)直線OM斜率的最小值為4;
;(Ⅲ)直線OM斜率的最小值為4;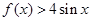 ,證明詳見解析.
,證明詳見解析.
解析試題分析:(Ⅰ)由已知,首先利用
科目:高中數(shù)學
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學
來源:
題型:解答題
已知函數(shù)
科目:高中數(shù)學
來源:
題型:解答題
如圖,某自來水公司要在公路兩側(cè)排水管,公路為東西方向,在路北側(cè)沿直線
科目:高中數(shù)學
來源:
題型:解答題
設
國際學校優(yōu)選 - 練習冊列表 - 試題列表 湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)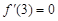 求出
求出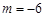 ,再由
,再由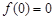 得
得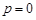 ,從而得
,從而得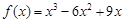 ,其導函數(shù)
,其導函數(shù)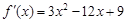 ,利用求函數(shù)極值的一般方法及一般步驟列表即可求得函數(shù)
,利用求函數(shù)極值的一般方法及一般步驟列表即可求得函數(shù) 的極大值和極小值;(Ⅱ)在(Ⅰ)的基礎上,分
的極大值和極小值;(Ⅱ)在(Ⅰ)的基礎上,分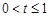 ,
,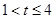 兩種情形討論.①當
兩種情形討論.①當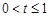 時,由(I)知
時,由(I)知 在
在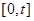 上遞增,所以
上遞增,所以 的最大值
的最大值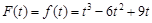 ,問題轉(zhuǎn)化為
,問題轉(zhuǎn)化為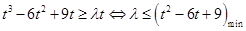 ;②當
;②當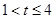 時,
時, 的最大值
的最大值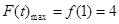 ,由
,由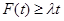 對任意的
對任意的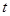 恒成立,等價于
恒成立,等價于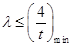 ,進而可求得
,進而可求得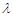 的取值范圍;(Ⅲ)由已知易得直線
的取值范圍;(Ⅲ)由已知易得直線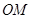 斜率
斜率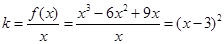 ,由于
,由于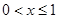 ,易得直線
,易得直線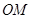 斜率的最小值為4.當
斜率的最小值為4.當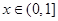 時,有
時,有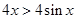 ,故
,故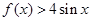 ,可以構造函數(shù)
,可以構造函數(shù)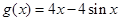 ,利用導數(shù)證明
,利用導數(shù)證明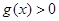 在
在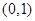 恒成立,從而證得
恒成立,從而證得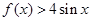 .
.
試題解析:(I)依題意,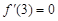 ,解得
,解得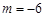 , 1分
, 1分
由已知可設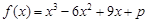 ,因為
,因為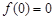 ,所以
,所以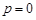 ,則
,則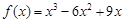 ,導函數(shù)
,導函數(shù)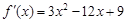 . 3分
. 3分
列表:
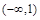
1 (1,3) 3 (3,+∞) 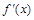
+ 0 - 


初中語文閱讀輕松組合周周練系列答案

劍橋小學英語系列答案
作業(yè)本江西教育出版社系列答案
新起點百分百單元測試卷系列答案
狀元口算計算系列答案
題庫精選系列答案
復習與測評單元綜合測試卷系列答案
小學畢業(yè)總復習北京教育出版社系列答案
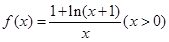
(I)函數(shù) 在區(qū)間
在區(qū)間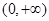 上是增函數(shù)還是減函數(shù)?證明你的結(jié)論;
上是增函數(shù)還是減函數(shù)?證明你的結(jié)論;
(II)當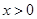 時,
時,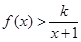 恒成立,求整數(shù)
恒成立,求整數(shù)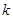 的最大值;
的最大值;
(Ⅲ)試證明: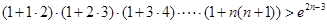
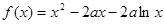 (
(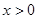 ,
,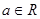 ),
),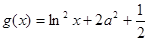 .
.
(Ⅰ)證明:當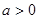 時,對于任意不相等的兩個正實數(shù)
時,對于任意不相等的兩個正實數(shù)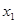 、
、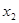 ,均有
,均有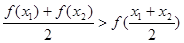 成立;
成立;
(Ⅱ)記 ,若
,若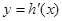 在
在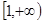 上單調(diào)遞增,求實數(shù)
上單調(diào)遞增,求實數(shù)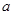 的取值范圍;
的取值范圍;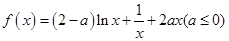 .
.
(1)當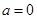 時,求
時,求 的極值;(2)當
的極值;(2)當 時,討論
時,討論 的單調(diào)性;
的單調(diào)性;
(3)若對任意的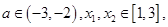 恒有
恒有 成立,求實數(shù)
成立,求實數(shù) 的取值范圍.
的取值范圍. 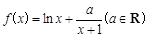 .
.
(1)當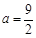 時,如果函數(shù)
時,如果函數(shù)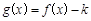 僅有一個零點,求實數(shù)
僅有一個零點,求實數(shù)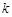 的取值范圍;
的取值范圍;
(2)當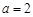 時,試比較
時,試比較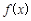 與1的大小;
與1的大小;
(3)求證: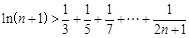
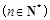
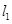 排水管,在路南側(cè)沿直線
排水管,在路南側(cè)沿直線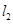 排水管(假設水管與公路的南,北側(cè)在一條直線上且水管的大小看作為一條直線),現(xiàn)要在矩形區(qū)域ABCD內(nèi)沿直線EF將
排水管(假設水管與公路的南,北側(cè)在一條直線上且水管的大小看作為一條直線),現(xiàn)要在矩形區(qū)域ABCD內(nèi)沿直線EF將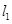 與
與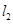 接通.已知AB = 60m,BC = 60
接通.已知AB = 60m,BC = 60 m,公路兩側(cè)排管費用為每米1萬元,穿過公路的EF部分的排管費用為每米2萬元,設EF與AB所成角為
m,公路兩側(cè)排管費用為每米1萬元,穿過公路的EF部分的排管費用為每米2萬元,設EF與AB所成角為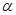 .矩形區(qū)域內(nèi)的排管費用為W.
.矩形區(qū)域內(nèi)的排管費用為W.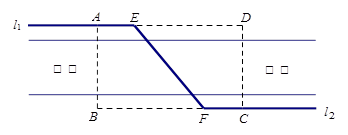
(1)求W關于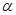 的函數(shù)關系式;
的函數(shù)關系式;
(2)求W的最小值及相應的角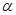 .
.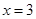 是函數(shù)
是函數(shù)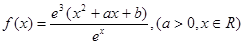 的一個極值點.
的一個極值點.
(1)求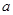 與
與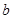 的關系式(用
的關系式(用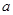 表示
表示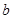 ),并求
),并求 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)設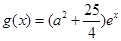 ,若存在
,若存在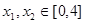 使得
使得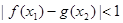 成立,求實數(shù)
成立,求實數(shù)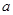 的取值范圍.
的取值范圍.
版權聲明:本站所有文章,圖片來源于網(wǎng)絡,著作權及版權歸原作者所有,轉(zhuǎn)載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯(lián)系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網(wǎng)安備42018502000812號